主机身份协议 (HIP) 是一种 3.5 层解决方案，最初旨在分离 IP 地址的双重角色 - 定位符和标识符。使用 HIP 协议不仅可以解决移动性问题，还可以在两个通信的终端主机之间建立经过身份验证的安全通道。在这篇短文中，我们首先介绍相关的背景信息。然后，我们介绍一些与椭圆曲线 (EC) 密码学和基于 EC 的 Diffie-Hellman 协议相关的数学背景。最后，我们展示了一些针对各种加密原语的微基准测试结果，并在文章结尾总结了 HIP 和 IPSec 的总体性能结果，我们使用 Python 语言在 Linux 用户空间中实现了这些协议。

引言

有时，使用 Python 或 Java 等高级语言在用户空间中实现原型更容易。在本文档中，我们尝试描述我们与主机身份协议版本 2 相关的实现工作。在第一部分，我们描述各种安全解决方案，然后我们讨论 HIP 协议的一些实现细节，最后，在这项工作的最后一部分，我们讨论使用 Python 语言实现的 HIP 和 IPSec 协议的性能。

背景

在本节中，我们将描述基本背景。首先，我们将讨论移动互联网的问题并介绍主机身份协议。然后，我们转到各种安全协议的讨论。我们将以讨论椭圆曲线和 Diffie-Hellman 算法的变体（使用 EC 密码学 (ECC)）来结束本节。

互联网最初的设计使得互联网协议 (IP) 地址扮演双重角色：它是定位符，以便路由器可以找到消息的接收者；它是标识符，以便上层协议（如 TCP 和 UDP）可以进行绑定（例如，传输层套接字使用 IP 地址和端口来建立连接）。当联网设备从一个网络漫游到另一个网络时，这就成了一个问题，因此 IP 地址会发生变化，导致上层连接失败。另一个问题是在通信方之间建立经过身份验证的通道。实际上，在建立连接时，各方的长期身份未得到验证。当然，有一些解决方案，例如 SSL，可以轻松解决手头的问题。但是，SSL 仅适用于 TCP 连接，并且大多数时候实际用例仅包括安全网络冲浪和 VPN 隧道的建立。另一方面，主机身份协议更加灵活：它允许对等方在网络层创建经过身份验证的安全通道，因此所有上层协议都可以从这种通道中受益。

HIP [13] 依赖于 4 次握手来建立经过身份验证的会话。在握手期间，对等方使用长期公钥相互验证身份，并使用 Diffie-Hellman 或椭圆曲线 (EC) Diffie-Hellman 算法派生会话密钥。为了对抗拒绝服务攻击，HIP 还引入了计算难题。HIP 使用公钥的截断哈希作为 IPv6 地址形式的标识符，并将此标识符公开给上层协议，以便应用程序可以建立常规连接（例如，应用程序可以打开常规 TCP 或 UDP 套接字连接）。同时，HIP 使用常规 IP 地址（支持 IPv4 和 IPv6）进行路由。因此，当主机的附件发生变化时（路由使用的 IP 地址也随之变化），暴露给应用程序的标识符保持不变。HIP 使用特殊的信令例程来通知相应的对等方定位符的更改。有关 HIP 的更多信息，请参见 RFC 7401 [15]。

如今有很多解决方案允许通信方相互验证身份并建立安全通道。在本节中，我们将回顾一些最广泛使用的安全协议，并讨论其应用用例。在这里，我们还将回顾一些允许终端主机分离 IP 地址双重角色的协议。

安全外壳协议 (SSH) 是一种安全解决方案 [5]。SSH 是应用层协议，为不安全网络提供加密通道。SSH 最初旨在提供安全的远程命令行、登录和命令执行。但实际上，任何网络服务都可以通过 SSH 进行保护。此外，SSH 还提供了在空间上分隔的网络之间创建 VPN 隧道的方法：SSH 是通过远程服务器转发本地流量的绝佳协议。但是，一旦网络设备更改其在网络中的连接点，该协议将失败。IPSec [12] 直接在 IP 协议之上运行，并提供两种不同的服务：(i) 它提供所谓的身份验证标头 (AH)，该标头仅用于身份验证，以及 (ii) 它提供封装安全有效载荷 (ESP)，这是一种身份验证加有效载荷加密机制。为了建立安全关联（协商密钥和算法），可以使用 IKE 或 IKEv2、ISAKMP 甚至预共享密钥和预先协商的安全算法集。

互联网密钥交换协议 (IKE) [6] 是 IPSec 中用于建立安全关联的协议，就像 HIP 一样。但是，与 HIP 不同，IKE 没有解决 IP 地址的双重角色问题。安全套接字层 (SSL) 是一种应用层解决方案，用于保护 TCP 连接的安全。SSL 在 RFC 6101 [4] 中进行了标准化。旨在防止窃听、中间人攻击、篡改和消息伪造。在 SSL 中，通信主机可以在长期身份（公钥证书）的帮助下相互验证身份。尽管我们上面列出的解决方案确实解决了 OSI [2] 模型各个层上的安全问题，但它们并非旨在处理节点移动性。因此，在下面的段落中，我们将列出几个专门为支持移动性并解决 IP 地址双重角色而设计的协议。

定位符标识符分离协议 (LISP) 在 RFC 6830 [8] 中进行了规定。在 LISP 中，标识符和定位符可以是任何内容：IPv4 地址、IPv6 地址、媒体访问控制地址等。除了分离定位符和标识符之外，一些优点还包括：地址族遍历（IPv4 over IPv4、IPv4 over IPv6、IPv6 over IPv6 甚至 IPv6 over IPv4）、移动性和改进的路由可伸缩性。

标识符/定位符网络协议 (ILNP) 在多个 RFC 中进行了规定。值得一看 RFC 6740 [16]，其中包含该协议的架构描述。ILNP 的主要优点是它提供增量部署，并且向后兼容 IP 协议。

移动 IP 是另一种处理节点移动性的协议。尽管该协议本身并未解决定位符和标识符分离问题，但我们仍将其归为此类，因为它解决了节点移动性期间出现的问题。因此，该协议最初旨在允许移动用户从一个网络移动到另一个网络，同时保持永久 IP 地址。该协议在 RFC 5944 [14]（对于 IPv4 协议）和 RFC 6275 [7]（对于 IPv6 协议）中进行了规定。但是，该协议的主要缺点是其复杂性。

现在，我们将继续讨论我们在使用 Python 语言实现主机身份协议时使用的密码库的局限性。

在我们编写本文时，密码库 (pycryptodome [3]) 在我们的实现中使用，不支持 Diffie-Hellman (DH) 和椭圆曲线 Diffie-Hellman (ECDH) 算法。因此，我们坐下来推导了我们自己对这些算法的实现。为了使事情更清楚一点，这里我们将提到一些关于椭圆曲线密码学 (ECC) 的背景知识（读者可以查看 [17] 以获取更多关于 EC 密码学的信息），并讨论 ECDH 的实现细节。

椭圆曲线具有以下形式 y²≡x³+ax+b mod p。为了使曲线至少有一个根，判别式应为非零。换句话说，δ=-16(4a³+27b²) ≢ 0 mod p，其中 p 是一个足够大的素数。通过定义一个二元运算（即加法运算），我们可以使椭圆曲线形成阿贝尔群。请记住，阿贝尔群具有以下属性：(i) 闭包性，意味着如果 A,B ∈ E，则 A+B ∈ E，(ii) 结合律：∀ A,B,C ∈ E 遵循 (A+B)+C=A+(B+C)。(iii) 存在单位元 I，使得 A+I=I+A=A，(iv) 存在逆元：∀A ∈ E A+A^-1=A^-1+A=I；(v) 交换律：∀A,B ∈ E A+B=B+A。最后，我们应该提到应该存在一个元素 G，使得该元素与其自身的多次加法 kG 生成群的所有其他元素。这样的群称为循环群。

让我们定义 O（无穷远点）为单位元，使得 P+O=O+P=P,∀P ∈E。此外，我们定义 P+(-P)=O，其中 -P=(x,-y)。接下来，假设 P,Q ∈ E，其中 P=(x₁,y₁) 且 Q=(x₂,y₂)。然后我们可以区分以下三种情况：(i) x₁≠ x₂（在这种情况下，通过给定两点的直线必须在某处与曲线相交于第三点 R=(x₃,y₃)），(ii) x₁=x₂ 且 y₁=-y（在这种情况下，直线是垂直的，并且不通过曲线上的第三点）；最后 (iii) x₁=x₂ 且 y₁=y₂（在这种情况下，直线与曲线相切，但仍然在第三点 R=(x₃,y₃) 处穿过曲线）。给定情况 (ii)，我们可以将负点定义为 -R=(x,-y)。

在第一种情况下，直线 L 通过点 P 和 Q。使用简单的几何图形，我们可以推导出直线的方程如下：y=βx+ν，其中 β=(y₂-y₁)(x₂-x₁)^-1

此外，我们可以找到 ν 为 ν=y₁-βx₁=y₂-βx₂

为了找到与曲线相交的点，我们可以将 y=βx+ν 代入椭圆曲线方程：(βx+ν)²=x³+ax+b

通过重新排列方程的项，我们得到：x³+ax+b-β² x²-2βνx-ν²=x³+(a-2βν)x-β² x²+b-ν²=0

但是由于得到的方程有三个根，我们有：(x-x₁)(x-x₂)(x-x₃)=x³-(x₃+x₂+x₁) x²+(x₂ x₃+x₁ x₃+x₁ x₂)x+x₁ x₂ x₃

通过注意到 β²=x₁+x₂+x₃，我们得到：x₃=β²-x₁-x₂

此外，由于 P+Q=-R，我们有：-y₃=β(x₃-x₁)+y₁ 或 y₃=β(x₁-x₃)-y₁

第二种情况很简单，根据定义，我们有 P-Q=O。最后，我们应该提到第三种情况很像第一种情况，但有一个区别 - 通过 P 和 Q 的直线与曲线相切，因为 P=Q。通过对椭圆曲线的原始函数应用隐式微分，我们得到：2y ∂y/∂x=3x₁²+a 由此我们可以推导出 β 如下：∂y/∂x=β=(3x₁²+a)(2y₁)^-1 此表达式允许我们推导出 x₃ 如下：x₃=β²-2x₁ 最后，就像第一种情况一样，我们有 y₃=β(x₁-x₃)-y₁。当然，所有运算都以素数 p 为模进行。

现在我们转到 ECDH 协议和一些实现细节的讨论。我们使用了 RFC5903 [9] 中定义的椭圆曲线参数。ECDH 按以下方式进行：甲方生成随机数 i，其中此随机数的大小等于构成素数 p 的字节数（这在参数集中指定）。乙方以类似的方式生成数字 j。双方都使用曲线 G 上的点（也是生成器，在 RFC5903 中指定），计算公钥：K_A=iG 和 K_B=jG。我们使用了著名的双倍和加法算法 [17] 来有效地计算乘法。接下来，双方交换公钥并派生共享密钥，如下所示 S=jK_A=iK_B=ijG。为了测试实现，我们使用了前面提到的 RFC 中提供的测试向量。

硬件和软件

对于硬件，我们使用了以下设置。我们使用单台机器作为发起方。该机器具有双核 Intel Celeron 处理器、16 GB 随机存取存储器 (RAM) 和 500 GB 硬盘驱动器。响应方是功能较弱的 Raspberry PI 微控制器，但具有四核 CPU，每个 CPU 以 1.0 GHz 运行，1 GB RAM 和用于持久存储的闪存卡。对于软件，我们在发起方上使用了 Ubuntu 18.04，在响应方上使用了 Raspbian OS。

我们已在 GitHub 存储库中公开了 HIPv2 协议的实现。感兴趣的读者可以在此处找到它 [11]。

实验评估

在本节中，我们将讨论 HIPv2 实现的性能相关问题。我们首先讨论一组微基准测试。因此，我们首先评估 ECDH 和 DH 算法的性能，然后切换到 RSA 和 ECDSA 签名算法的性能，最后讨论 AES 和 HMAC 算法的性能评估。之后，我们展示 HIP 实现的总体性能结果。

我们从难题计算的性能开始。在图 1 中，我们显示了难题解决方案计算的平均持续时间。显然，难度随着难题难度的增加呈指数增长。

图 1：难题解决的平均持续时间

 

图 2：Diffie-Hellman 密钥交换持续时间（总计）

为了演示 ECHD 和 DH 算法的性能，我们针对各种组执行了密钥交换算法 100 次。因此，在图 2 中，我们显示了 DH 的性能，在图 3 中，我们显示了 ECDH 对各种曲线参数的性能。为了理解两者之间的关系，我们在表 1 中显示了各种密钥的大小以及它们与对称密钥的关系。

图 3：椭圆曲线 Diffie-Hellman 密钥交换持续时间（总计）

对称密钥大小，比特	DH 密钥，比特	ECDH 密钥，比特
80	1024	160
112	2048	160
128	3072	256
192	7680	384
256	15360	521

表 1：密钥的安全强度

显然，ECDH 显示出比常规 DH 算法更好的性能。这种性能提升很大程度上是由于密钥尺寸的减小。接下来，我们测量了其他加密原语的计算性能。因此，在表 2 中，我们显示了我们完成的所有操作的汇总统计信息。

操作	平均时间，毫秒	中值时间，毫秒	标准差，毫秒
RSA（2048 位，SHA-256）签名	2.099	2.094	0.026
RSA（2048 位，SHA-256）验证	0.591	0.589	0.008
ECDSA（secp384r1，SHA-384）签名	1.379	1.374	0.042
ECDSA（secp384r1，SHA-384）验证	3.008	3.006	0.016
AES-256 加密	0.036	0.031	0.027
AES-256 解密	0.032	0.029	0.017
HMAC (SHA-256)	0.057	0.054	0.018

表 2：加密原语的性能

我们对每个加密原语执行了 100 轮测量。所有操作的数据大小均选择为 1500 字节。我们运行了 20 次 HIPv2 BEX，并测量了总的数据包处理时间（我们合并了发起方和响应方的数据包处理时间）。在图 4 中，我们显示了数据包处理持续时间的箱线图。为了运行测试，我们使用了以下配置：对于签名，我们使用了 2048 位长模数的 RSA，SHA-256 用于 HMAC 和哈希，NIST521 曲线的 ECDH，AES-256 用于加密，以及 16 位用于难题难度。我们注意到，处理 R1 数据包在响应方上消耗了相当多的时间。由于我们的实现缺少 R1 数据包的预创建，因此这种漫长的数据包处理时间是预期的。我们还测量了 HIPv2 基础交换 (BEX) 的总体持续时间。在图 4 中，我们显示了处理 HIP 数据包所需的时间，在图 5 中，我们演示了 HIP BEX 持续时间的分布。

图 4：数据包处理时间

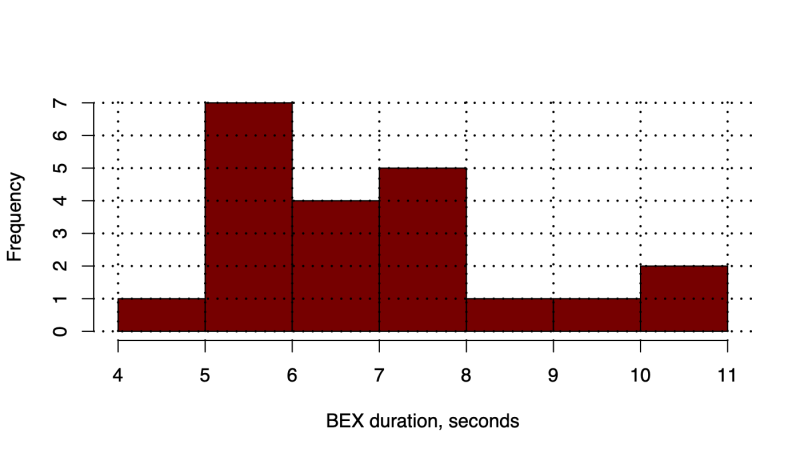
图 5：HIPv2 BEX 的持续时间

显然，使用 Python 等高级语言在用户空间中实现加密协议不是最佳选择：此类实现的性能对于生产服务器而言有些不可接受，最好使用 C 或 C++ 等较低级别的语言为过载的服务器实现安全解决方案。另一方面，Python 实现更适合学习和实验目的。最后，我们测量了 IPSec 隧道上的 TCP 连接和普通 TCP 的吞吐量。我们使用了 iperf [1] 工具来测量吞吐量。显然，通过我们的实现，我们能够实现的吞吐量略低于普通 TCP 连接获得的吞吐量的 25 倍（图 6）。对于 Python 实现的安全协议，预计会出现这样的结果。例如，在我们之前的研究 [10] 之一中，我们观察到我们的 Python VPN 实现也具有类似的行为。

图 6：通过 IPSec 和普通 TCP 连接获得的 TCP 吞吐量

结论

在这篇短文中，我们讨论了主机身份协议 (HIP) 的实现细节，HIP 是一种旨在分离 IP 地址双重角色的 3.5 层安全解决方案。HIP 协议不仅解决了 IP 地址角色分离的问题，而且还可以成为安全的移动性解决方案。HIP 在现代网络中有许多应用 - 从在固定网络实体之间建立安全通道到保护移动用户。我们创建了基于 Python 的最小 HIP 实现并对其进行了实验：(i) 我们进行了多次微基准测试，以及 (ii) 我们完成了该解决方案的几轮压力测试。我们还为 IPSec 实现了封装安全有效载荷 (ESP)，并通过使用 iperf 工具执行几轮带宽测量来测量总体性能。我们希望 HIP 的实现对其他人有用且有趣。为此，我们已将其公开在公共存储库 [11] 中。

参考文献

[1] iPerf - TCP、UDP 和 SCTP 的终极速度测试工具。https://iperf.fr/，2021 年。

[2] OSI 模型。https://en.wikipedia.org/wiki/OSI model，2021 年。

[3] PyCryptodome。https://pycryptodome.readthedocs.io/en/latest/，2021 年。

[4] A. Freier、P. Karlton、P. Kocher。安全套接字层 (SSL) 协议版本 3.0。https://datatracker.ietf.org/doc/html/rfc6101，2011 年。

[5] D. J. Barrett、R. E. Silverman 和 R. G. Byrnes。SSH，安全外壳：权威指南。O’Reilly Media, Inc.，2005 年。

[6] C. Kaufman、P. Hoffman、Y. Nir、P. Eronen。互联网密钥交换协议版本 2 (IKEv2)。https://datatracker.ietf.org/doc/html/rfc5996，2010 年。

[7] J. A. C. Perkins、D. Johnson。IPv6 中的移动性支持。https://datatracker.ietf.org/doc/html/rfc6275

[8] D. Farinacci、V. Fuller、D. Meyer、D. Lewis。定位符/ID 分离协议 (LISP)。https://datatracker.ietf.org/doc/html/rfc6830，2013 年。

[9] D. Fu 和 J. Solinas。用于 IKE 和 IKEv2 的模素数椭圆曲线组 (ECP 组)。https://datatracker.ietf.org/doc/html/ RFC5903，2010 年。

[10] D. Kuptsov。绕过深度数据包检测：通过 TLS VPN 隧道传输流量。https://linuxjournal.cn/content/bypassing-deep-packet-inspection-tunneling-traffic-over-tls-vpn，2021 年。

[11] D. Kuptsov。CuteHIP：主机身份协议的 Python 实现。https://github.com/dmitriykuptsov/cutehip，2021 年。

[12] N. Doraswamy 和 D. Harkins。IPSec：互联网、Intranet 和虚拟专用网络的新安全标准。Prentice Hall PTR，美国，1999 年。

[13] A. Gurtov。主机身份协议 (HIP)：迈向安全的移动互联网。Wiley 通信网络和分布式系统系列。Wiley，2008 年。

[14] C. Perkins。IPv4 的 IP 移动性支持，修订版。https://datatracker.ietf.org/doc/html/rfc5944

 

[15] R. Moskowitz、T. Heer、P. Jokela、T. Henderson。主机身份协议版本 2 (HIPv2)。https://datatracker.ietf.org/doc/html/rfc7401，2015 年。

[16] RJ Atkinson、SN Bhatti。标识符-定位符网络协议 (ILNP) 架构描述。https://datatracker.ietf.org/doc/html/rfc6740，2012 年。

[17] D. Stinson。密码学：理论与实践，第二版。CRC/C&H，第二版，2002 年。